
Mathematics
Statistics
Conditional Probability Calculator
Calculate the likelihood of an event A that is dependent on another event B using our easy-to-use conditional probability calculator!
The Schwarzschild radius calculator will calculate the distance from the center of a black hole beyond which nothing can escape its gravitational pull.
It is a fundamental property of a black hole and is also called the event horizon.
The mass of the black hole determines the Schwarzschild Radius. The other factors in the formula are constants: the Gravitational Constant (G) and the Speed of Light in a vacuum.
Using the Schwarzschild Radius Calculator, you can calculate the critical radius beyond which nothing can escape the gravitational pull of the black hole.
The variables in the calculator include
Mass of black hole (M) The mass of the black hole
Gravitational constant (G) The gravitational constant of
Speed of light (c) The speed of light in a vacuum
Schwarzschild Radius of Black Hole (R) We can calculate the Schwarzschild radius of a black hole by using the following formula
Any object, in order to escape a planet’s gravitational pull needs to be traveling at a minimum speed, and that speed is given by
Now, if the radius of the planet or star is small and the mass is significantly high, then the velocity required to escape the planet or star’s gravitational pull can be greater than the speed of light.
Black holes are the kind of entities that are incredibly dense and heavy objects with all of that mass confined to a small volume.
Karl Schwarzschild solved Einstein’s general theory of relativity to derive an expression for the critical radius beyond which nothing can escape the gravitational pull of a black hole. This critical radius is also known as the Schwarzschild Radius.
A star with a radius greater than the Schwarzschild radius, then light can escape from the surface of the planet or star.
Conversely, If all the body’s mass lies inside the Schwarzschild Radius, then the body is a black hole. Consequently, no light can escape from the surface of the black hole.
The Event Horizon is the distance from the black hole with the radius Rs.
You can calculate the Schwarzschild Radius using the following formula
Where,
Rs → Schwarzschild Radius of a Black Hole
G → Gravitational constant
M → Mass of a black hole
c → Speed of light in vacuum
Light cannot escape from inside the event horizon of a black hole. This is because the gravitational pull inside the event horizon is so strong that the escape velocity exceeds the speed of light.
Basically, anything that enters the event horizon cannot escape, and the blackhole will inevitably pull it back into itself. Once you’re in, you’re in for good.
The Schwarzschild radius was first discovered by the German physicist Karl Schwarzschild in 1916. He was the first to solve Einstein’s field equations of general relativity for a spherically symmetric object, which consequently led to the discovery of the Schwarzschild radius and the concept of a black hole.
The Schwarzschild radius is directly proportional to the mass of a black hole. It scales linearly with mass, and all that mass will be within the Schwarzschild radius.
The Schwarzschild radius is directly proportional to the mass of the black hole. The greater the black hole’s mass, the larger its Schwarzschild radius will be. However, based on the fact that space becomes more non-euclidean as we get closer to a black hole, we shouldn’t think about the radius in a literal sense.
Researchers use the Schwarzschild radius to understand the properties and behavior of black holes. It helps calculate the size and mass of black holes and determine the event horizon’s location.
Furthermore, scientists also employ it to study how black holes affect nearby matter and gain insights into the behavior of matter as it approaches and enters a black hole.

Mathematics
Statistics
Calculate the likelihood of an event A that is dependent on another event B using our easy-to-use conditional probability calculator!

Physics
Mechanics
Calculate the potential energy of the system using our elegant Potential Energy Calculator. Input the values required to find out!

Physics
Optics
Our nifty Snells law calculator helps you determine the refractive indices and angles of incidence and refraction with ease and precision.

Physics
Mechanics
Our Velocity calculator will help you calculate the object's velocity based on position and time values under constant acceleration.
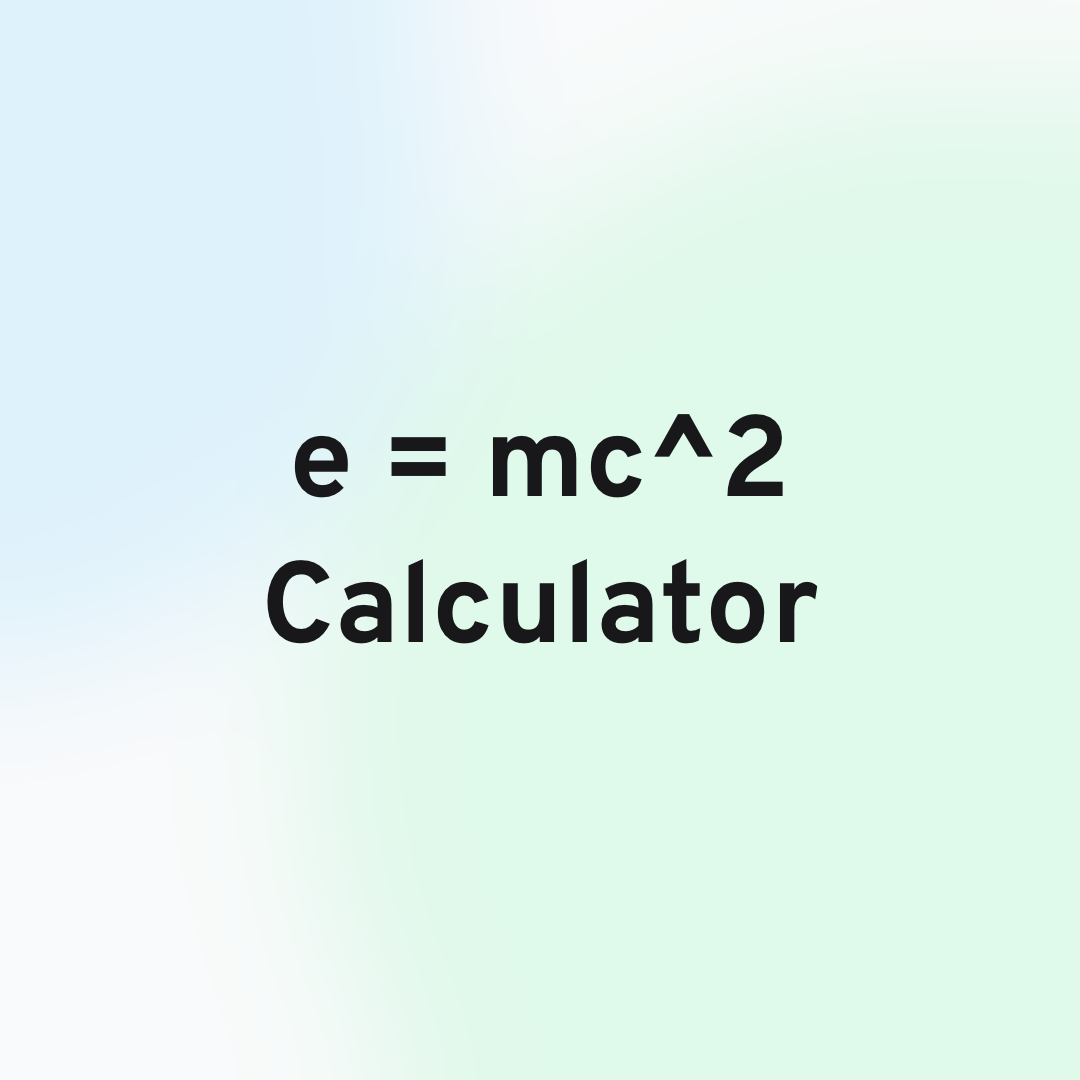
Physics
Modern Physics
Compute energy from Einstein's famous equation using our e=mc^2 (emc2) calculator. Input the mass and calculate the energy precisely.

Physics
Mechanics
Calculate the force of gravity between objects and understand the interactions between celestials using our Gravitational Force Calculator.